The most commonly used physical quantity for sound measurement is sound pressure. However, sound pressure magnitude is typically described using Sound Pressure Level (SPL). The audible range of sound pressure for the human ear is 2×10<sup>-5</sup> Pa to 20 Pa, corresponding to an SPL range of 0 dB to 120 dB. Therefore, introducing the concept of sound pressure level facilitates the description of sound pressure, which varies linearly over a very wide range.
1. Pressure
Definition: Pressure is defined as the force exerted per unit area.
Unit: The unit of pressure is Pascal (Pa).
1 Pa = 1 N/m² (i.e., 1 Pascal = 1 Newton of force applied over 1 square meter)
1Pa=103mPa=106µPa
2. Sound Pressure
1、When the atmosphere is disturbed by a sound wave, the atmospheric pressure changes from p0 to p1. The excess pressure resulting from this acoustic disturbance, p = p1 - p0, is termed Sound Pressure. The magnitude of sound pressure reflects the strength of the sound wave. Alternatively: The pressure generated by the vibration of sound through air is called sound pressure.Sound pressure is a scalar quantity, not a vector. Its phase is distinguished as positive or negative according to the following principle: when the sound pressure increases the total pressure, its phase is defined as positive; conversely, it is negative.
2、The unit of sound pressure is Pascal (Pa). Sometimes the unit bar is used, where 1 bar = 100 kPa.
3、The sound pressure value (20 µPa) at which a normal human ear can just perceive the existence of a 1 kHz sound is known as the Threshold of Hearing Sound Pressure for a 1 kHz tone. Generally, the human ear cannot detect the presence of sounds below this pressure value.
4、The sound pressure value at a specific instant in a sound field is called Instantaneous Sound Pressure.
5、The maximum instantaneous sound pressure value within a specified time interval is termed Peak Sound Pressure. If the sound pressure varies sinusoidally with time, the peak sound pressure corresponds to the amplitude of the sound pressure.
6、Within a specified time interval, the root mean square (RMS) value of the instantaneous sound pressure over time is called the Effective Sound Pressure
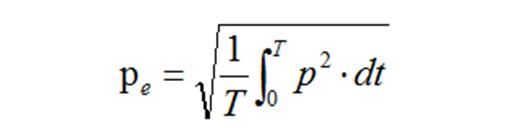
Where the subscript “e” denotes the effective value, and T represents the averaging time interval. T can be one period or a much longer interval. The sound pressure we commonly refer to and that measured by general electronic instruments is the effective sound pressure.
3. Sound Pressure Level (SPL)
3.1 Definition of Sound Pressure Level
Expressing the magnitude of sound by taking the logarithm of its effective sound pressure value yields the Sound Pressure Level (SPL). SPL is denoted by the symbol SPL and measured in decibels (dB):

Where pe is the effective value of the sound pressure being measured, and pref is the Reference Sound Pressure. In air, p<sub>ref</sub> is generally taken as 2×10-5 Pa (20 µPa).
Since the minimum sound pressure perceivable by the human ear is 20 µPa, this pressure is established as the reference standard, denoted pref. Therefore, in acoustics and medicine, 20 µPa = 0 dB SPL is defined as the Threshold of Hearing – the auditory "gate." Only sounds above this value can open this gate and be heard.
3.2 Calculation of Sound Pressure Level
The formula for calculating Sound Pressure Level in air is:
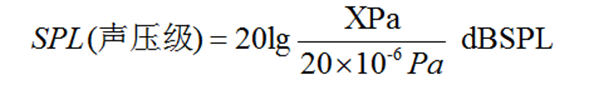
Example: SPL corresponding to a sound pressure of 1 Pa:
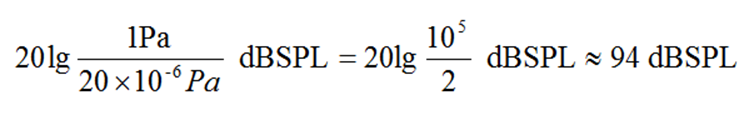
This is why we commonly say that a sound pressure of 1 Pa corresponds to 94 dB SPL. Similarly, we can calculate:
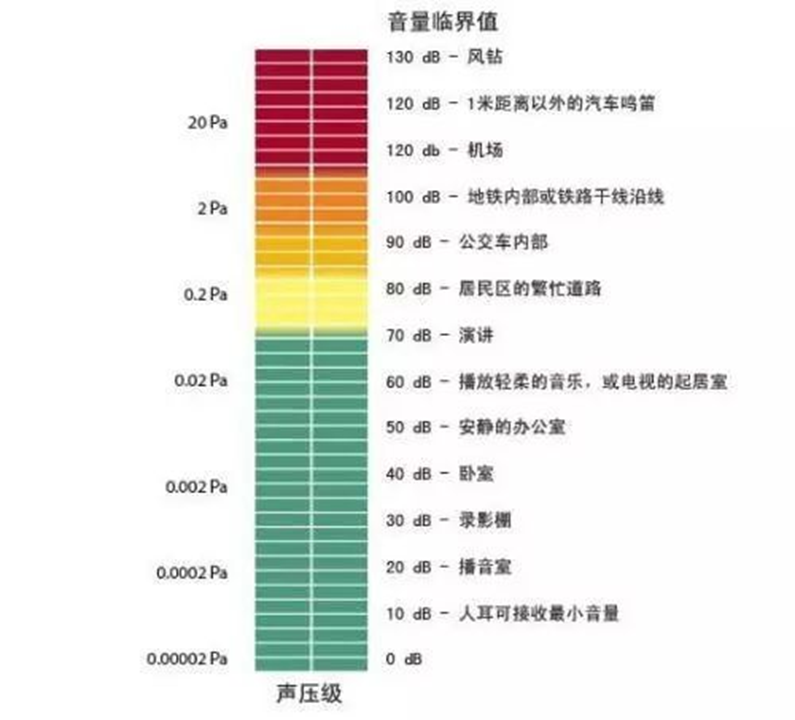
20µPa=0dBSPL
200µPa=20dBSPL
2mPa=40dBSPL
20mPa=60dBSPL
200mPa=80dBSPL
2Pa=100dBSPL
If the sound pressure increases by a factor of 10, the SPL increases by 20 dB. If the sound pressure doubles (factor of 2), the SPL increases by approximately 6 dB.
When the sound pressure reaches 20 Pa, corresponding to an SPL of 120 dB, the human ear experiences pain. Therefore, in acoustics and medicine, 20 Pa = 120 dB SPL is defined as the Threshold of Pain. Prolonged exposure to this environment can cause damage to the auditory system.
The primary reason for expressing acoustic quantities in decibels (dB) is that the human auditory system's response to sound intensity stimuli does not follow a linear (gradually increasing) pattern but rather a logarithmic proportional relationship. Using the logarithmic dB scale accommodates this characteristic of hearing. Secondly, the range of sound pressures encountered in daily life is very wide. Logarithmic conversion significantly compresses this range numerically, making the representation of acoustic quantities more practical and scientifically sound.